dw网页制作表格,百度seo软件优化,地板网站建设方案,龙岩网上办事大厅官网本节书摘来自华章出版社《 线性代数及其应用 #xff08;原书第4版#xff09;》一书中的第1章#xff0c;第1.2节#xff0c;作者:#xff08;美#xff09;戴维C. 雷#xff08;David C. Lay#xff09;马里兰大学帕克学院 著刘深泉 张万芹 陈玉珍 包乐娥 陆 博 译原书第4版》一书中的第1章第1.2节作者:美戴维C. 雷David C. Lay马里兰大学帕克学院 著刘深泉 张万芹 陈玉珍 包乐娥 陆 博 译更多章节内容可以访问云栖社区“华章计算机”公众号查看 1.2 行化简与阶梯形矩阵 本节我们将1.1节中的方法进一步精确化变成行化简算法也称行消去法它可用来解任意线性方程组. 1而应用算法的第一部分我们可以回答1.1节中提出的基本存在与唯一性问题. 这种算法可用于任意矩阵不管它是否为某一方程组的增广矩阵. 所以本节的第一部分讨论任意矩阵. 首先我们引入两类重要的矩阵它们包含1.1节中的“三角”矩阵在以下的定义中矩阵中非零行或列指矩阵中至少包含一个非零元素的行或列非零行的先导元素是指该行中最左边的非零元素. 定义 一个矩阵称为阶梯形或行阶梯形若它有以下三个性质 每一非零行在每一零行之上.某一行的先导元素所在的列位于前一行先导元素的右面.某一先导元素所在列下方元素都是零. 若一个阶梯形矩阵还满足以下性质称它为简化阶梯形或简化行阶梯形.每一非零行的先导元素是1.每一先导元素1是该元素所在列的唯一非零元素. 若一个矩阵具有阶梯形简化阶梯形它就称为阶梯形简化阶梯形矩阵. 性质2说明先导元素构成阶梯形. 性质3其实是性质2的推论不过我们把它列出来以示强调.1.1节中的“三角”矩阵如都是阶梯形的第二个矩阵是简化阶梯形的. 再举更多的例子. 例1 下列矩阵都是阶梯形的先导元素用 ? 表示它们可取任意的非零值在*位置的元素可取任意值包括零值. 下列矩阵是简化阶梯形的因先导元素都是1且在每个先导元素1的上、下各元素都是0. 一个矩阵可以行化简即用行初等变换变为阶梯形矩阵但用不同的方法可化为不同的阶梯形矩阵. 然而一个矩阵只能化为唯一的简化阶梯形矩阵. 下列定理将在书末附录A中给出证明. 定理1 简化阶梯形矩阵的唯一性每个矩阵行等价于唯一的简化阶梯形矩阵. 若矩阵A等价于阶梯形矩阵U称U为A的阶梯形或行阶梯形若U是简化阶梯形称U为A的简化阶梯形. 大部分矩阵程序用RREF作为简化行阶梯形的缩写有些用REF作为行阶梯形的缩写. 主元位置当矩阵经行变换化为阶梯形后经进一步的行变换将矩阵化为简化阶梯形时先导元素的位置并不改变. 因简化阶梯形是唯一的当给定矩阵化为任何一个阶梯形时先导元素总是在相同的位置上. 这些先导元素对应于简化阶梯形中的先导1. 定义 矩阵中的主元位置是A中对应于它的阶梯形中先导元素的位置. 主元列是A的含有主元位置的列. 在例1中符号?对应主元位置. 前四章中的许多基本概念都与矩阵中主元位置有联系. 例2 把下列矩阵A用行变换化为阶梯形确定主元列. 解 利用1.1节的方法. 最左边的非零列的第一个元素就是第一个主元位置. 这个位置必须放一个非零元即主元素. 最好将第一行与第四行对换这样可以避免分数运算. 把第一行的倍数加到其他各行以使主元1下面各元素变成0. 第二行的主元位置必须尽量靠左即在第二列. 我们选择这里的2作为第二个主元. 1 把第二行的-5/2倍加到第三行3/2倍加到第4行.  2 2中的矩阵与1.1节所遇到的不同这里没有办法在第3列中找到先导元素我们不能利用第一行或第二行否则会破坏已产生的阶梯形的先导元素的排列. 然而若我们对换第3行和第4行我们可在第4列产生先导元素. 此矩阵已是阶梯形. 第1、2、4列是主元列. 3 如例2所示主元就是在主元位置上的非零元素用来通过行变换把下面的元素化为0例2中的主元是12-5注意这些元素与矩阵A中同一位置的元素不相同如3式所示. 根据例2我们给出一个有效的算法变换矩阵成阶梯形或简化阶梯形. 认真掌握这一算法将使你获益匪浅. 行化简算法下列算法包含四个步骤它产生一个阶梯形矩阵第五步产生简化阶梯形矩阵. 我们用一个实例来说明这一算法. 例3 用行初等变换把下列矩阵先化为阶梯形再化为简化阶梯形. 解第一步由最左的非零列开始. 这是一个主元列. 主元位置在该列顶端. 第二步在主元列中选取一个非零元作为主元. 若有必要的话对换两行使这个元素移到主元位置上. 对换第1、3两行也可对换1、2两行 第三步用倍加行变换将主元下面的元素变成0. 我们当然可以把第1行除以主元3. 但这里第1列有两个3我们只需把第1行的-1倍加到第2行. 第四步暂时不管包含主元位置的行以及它上面的各行对剩下的子矩阵使用上述的三个步骤直到没有非零行需要处理为止. 暂时不看第一行第一步指出第2列是下一个主元列第二步我们选择该列中“顶端”的元素作为主元. 对第三步我们可先把子矩阵的“顶行”除以主元2. 不过也可以把这一行的-3/2倍加到下面的一行. 这就得到 暂时不看第二个主元所在的行我们剩下一个只有一行的新子矩阵. 新的子矩阵已不需要处理了我们已得到整个矩阵的阶梯形. 若我们需要简化阶梯形进行下一个步骤. 第五步由最右面的主元开始把每个主元上方的各元素变成0. 若某个主元不是1用倍乘变换将它变成1. 下一个主元在第2行将这行除以这个主元. 将第2行的9倍加到第1行 最后将第1行除以主元3 这就是原矩阵的简化阶梯形. ?第1~4步称为行化简算法的向前步骤产生唯一的简化阶梯形的第5步称为向后步骤. 数值计算的注解 在第2步中计算机程序通常选择一列中绝对值最大的元素作为主元. 这种方法通常称为部分主元法可以减少计算中的舍入误差. 线性方程组的解行化简算法应用于方程组的增广矩阵时可以得出线性方程组解集的一种显式表示法. 例如设某一个线性方程组的增广矩阵已经化为等价的简化阶梯形 因为增广矩阵有4列所以有3个未知数对应的线性方程组是 4对应于主元列的变量 和 称为基本变量 .1其他变量如 称为自由变量.当一个线性方程组是相容的如方程组4解集可以用显式表示只要把方程的简化形式解出来用自由变量表示基本变量即可. 由于简化阶梯形使每个基本变量仅包含在一个方程中这是很容易的. 在方程组4中我们可由第1个方程解出 第2个方程解出 第3个方程对未知数没有任何限制可以不管它. 5我们说 是自由变量是指它可取任意的值. 当 的值选定后由5中的前2个方程就可以确定 和 的值例如当 0得出解140当 得出解631 的不同选择确定了方程组的不同的解方程组的每个解由 的值的选择来确定. 5式给出的解称为方程组的通解因为它给出了所有解的显式表示. 例4 求方程组的解该方程组的增广矩阵已经化为解 该矩阵已是阶梯形但我们在解出基本变量前仍需把它化为简化阶梯形记号“~”表示它前面和后面的两个矩阵是行等价的译者注该记号在中文教科书中并未通用.增广矩阵有6列所以原方程组有5个变量对应的方程组为 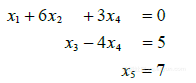 6 矩阵的主元列是第135列基本变量为 剩下的变量 和 为自由变量解出基本变量我们得通解为  7 注意由方程组6的第3个方程 的值是确定的. 解集的参数表示解集的表示式5和7称为解集的参数表示其中自由变量作为参数. 解方程组就是要求出解集的这种参数表示或确定它无解. 当一个方程组是相容的且具有自由变量则它的解集具有多种参数表示. 例如在方程组4中我们可以把方程2的5倍加到方程1得等价方程组这时可把 看作参数用 表示 和 得到解集的第一种表示法. 不过我们总是约定使用自由变量作为参数来表示解集本书末尾的习题解答也采用这一约定. 当方程组是不相容时解集是空集无论方程组是否有自由变量此时解集无参数表示. 回代考虑下列方程组它的增广矩阵已是阶梯形但还不是简化阶梯形计算机程序通常用回代法解此方程组而不是求它的简化阶梯形. 也就是说程序先解第3个方程用 表示 并把此表达式代入第2个方程从中解出 最后把 和 的表达式代入第1个方程解出 . 我们的矩阵算法即行化简算法的向后步骤它求出简化阶梯形与回代法所需算术运算次数相同. 但矩阵算法通常减少了手算时出错的可能性. 我强烈建议你仅使用简化阶梯形来解方程组与本书配合的学习指导书给出一些好的建议帮助你更快更准确地解方程组. 数值计算的注解 一般地行化简算法的向前步骤比向后步骤需要更多运算. 解方程组的算法通常用浮算来衡量. 一个浮算flop或浮点运算就是两个浮点实数进行一次算术运算-*/. 对一个矩阵化简为阶梯形大约需要 次浮算当 n相当大比如说n30 时大约是 次浮算而进一步化为简化阶梯形大约最多只需n2次浮算. 存在与唯一性问题虽然非简化的阶梯形并不适于解线性方程组这种形式对于回答1.1节中提出的两个基本问题已经足够了. 例5 确定下列线性方程组的解是否存在且唯一 解 该方程组的增广矩阵在例3中化简为  8 基本变量是 自由变量是 . 这里没有类似01的造成不相容方程组的方程所以我们可用回代法求解. 但解的存在性在方程8中已经清楚了. 同时解不是唯一的因为有自由变量存在. 的每一种选择都确定一组解所以此方程组有无穷多组解. 当一个方程组化为阶梯形且不包含形如0b 的方程其中 每个方程包含一个基本变量它的系数非零. 或者这些基本变量已完全确定此时无自由变量或者至少有一个基本变量可用一个或多个自由变量表示对前一种情形有唯一的解对后一种情形有无穷多个解对应自由变量的每一个选择都有一个解. 上述讨论证明了以下定理定理2 存在与唯一性定理线性方程组相容的充要条件是增广矩阵的最右列不是主元列. 也就是说增广矩阵的阶梯形没有形如的行若线性方程组相容它的解集可能有两种情形ⅰ当没有自由变量时有唯一解 ⅱ若至少有一个自由变量有无穷多解. 以下是求解线性方程组的步骤. 应用行化简算法解线性方程组 写出方程组的增广矩阵.应用行化简算法把增广矩阵化为阶梯形. 确定方程组是否有解如果没有解则停止否则进行下一步.继续行化简算法得到它的简化阶梯形.写出由第3步所得矩阵所对应的方程组.把第4步所得的每个方程改写为用自由变量表示基本变量的形式. 练习题求出下列增广矩阵对应的方程组的解求出下列方程组的通解习题1.2 练习题答案 增广矩阵的简化阶梯形和相应的方程组是基本变量是 与 通解为见图1-6 注意要点是一般解要描述每个变量参数要明显标出. 下面的写法是不正确的 在这种写法中似乎和 都是自由变量这当然是不对的. 当我们行化简方程组的增广矩阵得所得阶梯矩阵说明方程是不相容的因它的最右列是主元列第3行相应于方程05因此不必再进行任何行变换. 注意自由变量在此问题中并不起作用因为方程组是不相容的.