建网站淄博,丰台网站制作,进一步加强区门户网站建设管理办法,seo关键词排名优化哪好文章目录 0.简介1.常用术语1) 模型2) 数据集3) 样本特征4) 向量5) 矩阵6)假设函数损失函数7#xff09;拟合过拟合欠拟合 2.线性回归3.梯度下降求极值4.Logistic回归算法#xff08;分类问题#xff09;5.KNN最邻近分类算法6.朴素贝叶斯分类算法7.决策树… 文章目录 0.简介1.常用术语1) 模型2) 数据集3) 样本特征4) 向量5) 矩阵6)假设函数损失函数7拟合过拟合欠拟合 2.线性回归3.梯度下降求极值4.Logistic回归算法分类问题5.KNN最邻近分类算法6.朴素贝叶斯分类算法7.决策树分类算法8.信息熵9.支持向量机SVM分类算法 0.简介 机器学习Machine Learning简称 ML是人工智能领域的一个分支也是人工智能的核心其涉及知识非常广泛比如概率论、统计学、近似理论、高等数学等多门学科。 就当下而言Python 无疑是机器学习领域最火的编程语言这得益于 Python 对科学计算的强大支持。因此本套教程中关于机器学习算法的代码均采用 Python 机器学习库 sklearn 编写。 机器学习的最主要的一项工作就是“训练模型”训练模型的过程就是机器学习算法实现的过程这里的算法和我们经常提及的算法有些区别比如插入排序、归并排序等它们的结果都是“计算出来的”只要确定输入就可以给定一个值而机器学习的算法是“猜”出来的既然是猜那么就会有对有错机器学习会根据猜的“结果”不断的优化模型从而得出正确率最高的“结果”。 机器学习的学习形式可以分为两大类
有监督学习无监督学习 每一类学习形式都对应着相应的算法比如线性回归算法、KNN 分类算法、朴素贝叶斯分类算法、支持向量机算法等等并且这些算法都有与其相适用的场景本套教程将对上述算法的原理和应用做详细的介绍。
1.常用术语
1) 模型 模型这一词语将会贯穿整个教程的始末它是机器学习中的核心概念。你可以把它看做一个“魔法盒”你向它许愿输入数据它就会帮你实现愿望输出预测结果。整个机器学习的过程都将围绕模型展开训练出一个最优质的“魔法盒”它可以尽量精准的实现你许的“愿望”这就是机器学习的目标。
2) 数据集 数据集从字面意思很容易理解它表示一个承载数据的集合如果说“模型”是“魔法盒”的话那么数据集就是负责给它充能的“能量电池”简单地说如果缺少了数据集那么模型就没有存在的意义了。数据集可划分为“训练集”和“测试集”它们分别在机器学习的“训练阶段”和“预测输出阶段”起着重要的作用。
3) 样本特征 样本指的是数据集中的数据一条数据被称为“一个样本”通常情况下样本会包含多个特征值用来描述数据比如现在有一组描述人形态的数据“180 70 25”如果单看数据你会非常茫然但是用“特征”描述后就会变得容易理解如下所示 图1样本特征 由上图可知数据集的构成是“一行一样本一列一特征”。特征值也可以理解为数据的相关性每一列的数据都与这一列的特征值相关。 4) 向量 任何一门算法都会涉及到许多数学上的术语或者公式。在本教程写作的过程中也会涉及到很多数学公式以及专业的术语在这里我们先对常用的基本术语做一下简单讲解。 第一个常用术语就是“向量”向量是机器学习的关键术语。向量在线性代数中有着严格的定义。向量也称欧几里得向量、几何向量、矢量指具有大小和方向的量。您可以形象地把它的理解为带箭头的线段。箭头所指代表向量的方向线段长度代表向量的大小。与向量对应的量叫做数量物理学中称标量数量只有大小没有方向。 在机器学习中模型算法的运算均基于线性代数运算法则比如行列式、矩阵运算、线性方程等等。其实对于这些运算法则学习起来并不难它们都有着一定运算规则只需套用即可因此你也不必彷徨可参考向量运算法则。向量的计算可采用 NmuPy 来实现如下所示
import numpy as np
#构建向量数组
anp.array([-1,2])
bnp.array([3,-1])#加法
a_bab
#数乘
a2a*2
b3b*(-3)
#减法
b_aa-b
print(a_b,a2,b3,b_a)输出结果 [2 1] [-2 4] [-9 3] [-4 3] 简而言之数据集中的每一个样本都是一条具有向量形式的数据。
5) 矩阵 矩阵也是一个常用的数学术语你可以把矩阵看成由向量组成的二维数组数据集就是以二维矩阵的形式存储数据的你可以把它形象的理解为电子表格“一行一样本一列一特征”表现形式如下 图2矩阵表格 如果用二维矩阵的表示的话其格式如下所示 6)假设函数损失函数 假设函数和损失函数是机器学习中的两个概念它并非某个模块下的函数方法而是我们根据实际应用场景确定的一种函数形式就像你解决数学的应用题目一样根据题意写出解决问题的方程组。下面分别来看一下它们的含义。 ①假设函数 假设函数Hypothesis Function可表述为yf(x)其中 x 表示输入数据而 y 表示输出的预测结果而这个结果需要不断的优化才会达到预期的结果否则会与实际值偏差较大。 ②损失函数 损失函数Loss Function又叫目标函数简写为 L(x)这里的 x 是假设函数得出的预测结果“y”如果 L(x) 的返回值越大就表示预测结果与实际偏差越大越小则证明预测值越来越“逼近”真实值这才是机器学习最终的目的。因此损失函数就像一个度量尺让你知道“假设函数”预测结果的优劣从而做出相应的优化策略。 ③优化方法 “优化方法”可以理解为假设函数和损失函数之间的沟通桥梁。通过 L(x) 可以得知假设函数输出的预测结果与实际值的偏差值当该值较大时就需要对其做出相应的调整这个调整的过程叫做“参数优化”而如何实现优化呢这也是机器学习过程中的难点。其实为了解决这一问题数学家们早就给出了相应的解决方案比如梯度下降、牛顿方与拟牛顿法、共轭梯度法等等。因此我们要做的就是理解并掌握“科学巨人”留下的理论、方法。 7拟合过拟合欠拟合
①拟合 形象地说“拟合”就是把平面坐标系中一系列散落的点用一条光滑的曲线连接起来因此拟合也被称为“曲线拟合”。拟合的曲线一般用函数进行表示但是由于拟合曲线会存在许多种连接方式因此就会出现多种拟合函数。通过研究、比较确定一条最佳的“曲线”也是机器学习中一个重要的任务。如下图所示展示一条拟合曲线蓝色曲线 图4曲线拟合 ②过拟合 过拟合overfitting与是机器学习模型训练过程中经常遇到的问题所谓过拟合通俗来讲就是模型的泛化能力较差也就是过拟合的模型在训练样本中表现优越但是在验证数据以及测试数据集中表现不佳。 举一个简单的例子比如你训练一个识别狗狗照片的模型如果你只用金毛犬的照片训练那么该模型就只吸纳了金毛狗的相关特征此时让训练好的模型识别一只“泰迪犬”那么结果可想而知该模型会认为“泰迪”不是一条狗。如下图所示 图5过拟合 过拟合问题在机器学习中经常遇到主要是因为训练时样本过少特征值过多导致的后续还会详细介绍。 ③欠拟合 欠拟合underfitting恰好与过拟合相反它指的是“曲线”不能很好的“拟合”数据。在训练和测试阶段欠拟合模型表现均较差无法输出理想的预测结果。如下图所示 图6欠拟合 造成欠拟合的主要原因是由于没有选择好合适的特征值比如使用一次函数ykxb去拟合具有对数特征的散落点ylog2x示例图如下所示 图7欠拟合示例图 欠拟合和过拟合是机器学习中会遇到的问题这两种情况都不是我期望看到的因此要避免。 2.线性回归
线性回归主要用来解决回归问题也就是预测连续值的问题。而能满足这样要求的数学模型被称为“回归模型”。最简单的线性回归模型是我们所熟知的一次函数即 ykxb这种线性函数描述了两个变量之间的关系其函数图像是一条连续的直线。如下图蓝色直线 图1线性连续函数 还有另外一种回归模型也就是非线性模型(nonlinear model)它指因变量与自变量之间的关系不能表示为线性对应关系(即不是一条直线)比如我们所熟知的对数函数、指数函数、二次函数等。 图2非线性连续函数 下面通过一个具体实例讲解线性回归预测的具体流程。 数据采集 任何模型的训练都离不开数据因此收集数据构建数据集是必不可少的环节。比如现在要预测一套房子的售价那么你必须先要收集周围房屋的售价这样才能确保你预测的价格不会过高或过低。如下表所示 当然上述样本数量远远不足如果想要更加准确的预测就要收集更多的数据至少保证 100 条样本。表格中的最后一栏是“房屋售价”这是“有监督学习”的典型特点被称为“标签”也就是我们所说的“参考答案”。表格中的面积、数量、距离市中心距离km以及是否是学区房这些都是影响最终预测结果的相关因素我们称之为“特征”也叫“属性”。 你可能会认为影响房屋售价的不止这些因素没错不过采集数据是一个很繁琐的过程因此一般情况下我们只选择与预测结果密切相关的重要“特征”。 构建线性回归模型 有了数据以后下一步要做的就是构建线性回归模型这也是最为重要的一步这个过程会涉及到一些数学知识至于如何构建模型下一节会做详细介绍。 构建完模型我们需要对其进行训练训练的过程就是将表格中的数据以矩阵的形式输入到模型中模型则通过数学统计方法计算房屋价格与各个特征之间关联关系也就是“权值参数”。训练完成之后您就可以对自己的房屋价格进行预测了。首先将数据按照“特征值”依次填好并输入到模型中最后模型会输出一个合理的预测结果。示意图如下所示 一次函数就是最简单的“线性模型”其直线方程表达式为y kx b其中 k 表示斜率b 表示截距x 为自变量y 表示因变量。函数中斜率 k 与 截距 b 控制着“直线”的“旋转”与“平移”。如果斜率 k 逐渐减小则“直线”会向着“顺时针”方向旋转为 k 0 的时候与 x 轴平行。截距 b 控制“直接”的上下平移b 为正数则向上平移b 为负数则表示向下平移。在机器学习中斜率 k 通常用 w 表示也就是权重系数因此“线性方程”通过控制 w 与 b 来实现“直线”与数据点最大程度的“拟合”。 线性方程不能完全等同于“直线方程”因为前者可以描述多维空间内直接而后者只能描述二维平面内的 x 与 y 的关系。 在线性回归问题中数据样本会呈现“线性”分布的态势因此我们使用“线性方程”来最大程度的“拟合数据”。线性方程预测的结果具有连续性下面通过示例简单说明小亮今年 8 岁去年 7 岁前年 6 岁那么他明年几岁呢估计你闭着眼都能想到答案但是我们要从机器学习的角度去看待这个问题。 首先年龄、时间是一组连续性的数据也就是因变量随着自变量规律性地连续增长显然它是一个“回归问题”。下面把上述数据以二维数组的形式表示出来构建一个数据集如下所示 [[2021,8], [2020,7], [2019,6]] 我们知道两个点就可以确定一条“直线”因此将两组数据带入 y kx b最终求得“线程方程” y x - 2013 上述函数就是所谓的“假设函数”通过它即可实现对结果的预测。从上述函数图像可以看出直线对数据样本恰好“拟合”。这是最标准的拟合直线通过它就可以“预测”出小亮明年的年龄了。上述示例就构建了一个简单的的“线性模型”。读到这里你会惊叹“怎么如此简单”其实线性模型就是这么简单。对于机器学习而言最关键的就是“学习”在大量的数据中通过不断优化参数找到一条最佳的拟合“直线”最终预测出一个理想的结果。 提示上述示例是一个理想化的“线性模型”在实际应用中要复杂的多不过“万变不离其宗” 机器学习是一门数学、统计学、计算机科学的结合技术因此它有着独特的知识体系比如会将数据集分为“训练集”与“测试集”而且还会通过“损失函数”来不断优化预测结果 通过前面知识的学习我们知道假设函数是用来预测结果的。前面讲述时为了让大家更容易理解“线性回归”我们以“直线方程”进行了类比讲解然而线性方程并不等同于“直线方程”线性方程描绘的是多维空间内的一条“直线”并且每一个样本都会以向量数组的形式输入到函数中因此假设函数也会发生一些许变化函数表达式如下所示 Y 1 w T X 1 b Y_{1}w^{T}X_{1}b Y1wTX1b 这个标量公式换成了向量的形式。 Y 1 Y_{1} Y1仍然代表预测结果 X 1 X_{1} X1表示数据样本 b b b表示用来调整预测结果的“偏差度量值”而 Y w T Yw^{T} YwT表示权值系数的转置。 损失函数就像一个衡量尺这个函数的返回值越大就表示预测结果与真实值偏差越大。其实计算单个样本的误差值非常简单只需用预测值减去真实值即可 l o s s ∑ ( w T X 1 b − Y ) 2 n loss\frac{\sum(w^{T}X_{1}b-Y)^{2}}{n} lossn∑(wTX1b−Y)2 但是上述方法只适用于二维平面的直线方程。在线性方程中要更加复杂、严谨一些因此我们采用数学中的“均方误差”公式来计算单样本误差在机器学习中使用损失函数的目的是为了使用“优化方法”来求得最小的损失值这样才能使预测值最逼近真实值。
3.梯度下降求极值 我们最终的目的要得到一个最佳的“拟合”直线因此就需要将损失函数的偏差值减到最小我们把寻找极小值的过程称为“优化方法”常用的优化方法有很多比如共轭梯度法、梯度下降法、牛顿法和拟牛顿法。 导数也叫导函数或者微商它是微积分中的重要基础概念从物理学角度来看导数是研究物体某一时刻的瞬时速度比如你开车从家 8:00 出发到公司上班9:00 到到达公司这一个小时内的平均车速是 80km/h而途中8:15:30这一时刻的速度就被称为瞬时速度此刻的速度可能是 100km/h也可能是 20km/h。而从几何意义上来讲你可以把它理解为该函数曲线在一点上的切线斜率。 导数有其严格的数学定义它巧妙的利用了极限的思想也就是无限趋近于 0 的思想。设函数 yf(x) 在点 x0 的某个邻域内有定义当自变量 x 在 x0 处有增量 Δx(x0Δx也在该邻域内时相应地函数取得增量 Δyf(x0Δx)-f(x0)如果 Δy 与 Δx 之比当 Δx→0 时极限存在则称函数 yf(x) 在点 x0 处可导并称这个极限为函数 yf(x) 在点 x0 处的导数记做 那么什么样的函数具有导数呢是不是所有的函数都有导数当然不是而且函数也不一定在其所有点上都有导数。如果某函数在某一点导数存在则称其在这一点可导否则称为不可导。可导的函数一定连续不连续的函数一定不可导。导数的发明者是伟大的科学家牛顿与布莱尼茨它是微积分的一个重要的支柱。在机器学习中我们只需会用前辈科学家们留下来的知识就行了比如熟悉常见的导函数公式以下列举了常用的导数公式 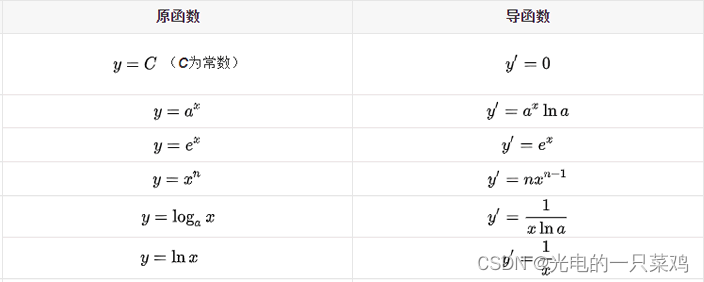 偏导数虽然和导数只有一字之差但是却相差甚多从它们的定义来看偏导数是指对含有两个自变量的函数中的一个自变量求导也就是说偏导数要求函数必须具备两个自变量。比如拿 zf(x,y) 举例如果只有自变量x变化而自变量y固定即看作常量这时它就是x的一元函数这函数对x的导数就称为二元函数z对于x的偏导数记做 fx(x,y) 。 梯度下降是机器学习中常用的一种优化方法主要用来解决求极小值的问题某个函数在某点的梯度指向该函数取得最大值的方向那么它的反反向自然就是取得最小值的方向。在解决线性回归和 Logistic逻辑 回归问题时梯度下降方法有着广泛的应用。梯度是微积分学的术语它本质上是一个向量表示函数在某一点处的方向导数上沿着特定的方向取得最大值即函数在该点处沿着该方向变化最快变化率最大。梯度下降法的计算过程就是沿梯度方向求解极小值当然你也可以沿梯度上升的方向求解极大值。那么如何能够更好的理解“梯度下降”呢如果不考虑其他外在因素其实你可以把它想象成“下山”的场景如何从一个高山上以最快的时间走到山脚下呢其实很简单以你所在的当前位置为基准寻找该位置最陡峭的地方然后沿着此方向向下走并且每走一段距离都要寻找当前位置“最陡峭的地方”反复采用上述方法最终就能以最快的时间抵达山脚下。从上述描述中你可能感觉到平淡无奇其实每一个词语都蕴含着数学知识比如“以当前所在位置为基准找到最陡峭的地方”从数学角度来讲就是找到所在点的“切线”方向也就是对这点“求导”然后循着切线轨迹点反复使用此方法就可以到达极小值点。 因此“梯度下降”就需要控制损失函数的w和b参数来找到最小值。比如控制 w 就会得到如下方法 w新w旧 - 学习率 * 损失值 通过梯度下降计算极小值时需要对损失函数的w求偏导求得这个偏导也就是“梯度”通过损失值来调节w不断缩小损失值直到最小这也正是梯度下降的得名来由。“学习率”是一个由外部输入的参数被称为“超参数”可以形象地把它理解为下山时走的“步长”大小想要 w 多调整一点就把学习率调高一点。不过学习率也不是越高越好过高的学习率可能导致调整幅度过大导致无法求得真正的最小值。当损失函数取得极小值时此时的参数值被称为“最优参数”。因此在机器学习中最重要的一点就是寻找“最优参数”。梯度下降是个大家族它有很多成员比如批量梯度下降BGD、随机梯度下降SGD、小批量梯度下降MBGD其中批量梯度下降是最常用的。
4.Logistic回归算法分类问题 其实想要理解“分类”问题非常的简单我们不妨拿最简单的“垃圾分类处理”的过程来认识一下这个词。现在考虑以下场景 小明拎着两个垃圾袋出门倒垃圾等走到垃圾回收站的时候小明发现摆放着两个垃圾桶上面分别贴着“可回收”与“不可回收”。小明经过自己的判断后把自己右手的垃圾放进了贴有“不可回收”的垃圾桶内而左手的垃圾袋放进了“可回收”的垃圾桶内最终完成了这次倒垃圾的过程。 其实上述“倒垃圾”的案例就说明了“分类问题”的过程。“可回收”与“不可回收”是两种预测分类而小明是主观判断的个体他通过自己日常接触的知识对“垃圾种类”做出判断我们把这个程称作“模型训练”只有通过“训练”才可以更加准确地判断“垃圾”的种类。小明进行了两次投放动作每一次投放都要对“垃圾”种类做出预先判断最终决定投放到哪个垃圾桶内。这就是根据模型训练的结果进行预测的整个过程。 下面对上述过程做简单总结 类别标签“可回收”与“不可回收”。 模型训练以小明为主体把他所接受的知识、经验做为模型训练的参照。 预测投放垃圾的结果预测分类是否正确。并输出预测结果。 分类问题是当前机器学习的研究热点它被广泛应用到各个领域比图像识别、垃圾邮件处理、预测天气、疾病诊断等等。“分类问题”的预测结果是离散的它比线性回归要更加复杂那么我们应该从何处着手处理“分类问题”呢这就引出了本节要讲的 Logistic 回归分类算法。 Logistic 回归算法又叫做逻辑回归算法或者 LR 算法Logistic Regression。分类问题同样也可以基于“线性模型”构建。“线性模型”最大的特点就是“直来直去”不会打弯而我们知道分类问题的预测结果是“离散的”即对输出数据的类别做判断。比如将类别预设条件分为“0”类和“1”类或者“是”或者“否”那么图像只会在 “0”和“1”之间上下起伏如下图所示 此时你就可能会有很多疑问线性回归函数不可能“拟合”上述图像。没错所以接下来我们要学习另一个线性函数 Logistic 函数。 注意在机器学习中Logistic 函数通常用来解决二元分类问题也就是涉及两个预设类别的问题而当类别数量超过两个时就需要使用 Softmax 函数来解决。 19 世纪统计学家皮埃尔·弗朗索瓦·韦吕勒发明了 Logistic 函数该函数的叫法有很多比如在神经网络算法中被称为 Sigmoid 函数也有人称它为 Logistic 曲线。其函数图像如下所示 该函数图像的数学表达式如下 l o g i s t i c ( z ) 1 1 e − z logistic(z)\frac{1}{1e^{-z}} logistic(z)1e−z1 e 称为自然常数也就是一个固定值的“常量”e-z 是以 e 为底、z 为变量的指数函数还可以写为 e-x 在编写程序代码时通常将其写为 exp(-x)。至于这个表达式是如何推断出来的我们没有必要深究学会站在“巨人”的肩膀上学习也是一种难得的品质。Logistic 函数也称为 S 型生长曲线取值范围为 (0,1)它可以将一个实数映射到 (0,1) 的区间非常适合做二元分类。当 z0 时该函数的取值为 0.5随着 z 的增大对应的函数值将逼近于 1而随着 z 的减小其函数值将逼近于 0。对于 Logistic 函数而言坐标轴 0 是一个有着特殊意义坐标越靠近 0 和越远离 0 会出现两种截然不同的情况任何大于 0.5 的数据都会被划分到 “1”类中而小于 0.5 会被归如到 “0”类。因此你可以把 Logistic 看做解决二分类问题的分类器。如果想要 Logistic 分类器预测准确那么 x 的取值距离 0 越远越好这样结果值才能无限逼近于 0 或者 1。 Logistic 函数能够很好的拟合“离散数据”因此可以把它看做“假设函数”但是还需要稍稍的改变一下形式如下所示 l o g i s t i c ( z ) 1 1 e − w T x i b logistic(z)\frac{1}{1e^{-w{T}x_{i}b}} logistic(z)1e−wTxib1上述公式和 Logistic 函数基本一致只不过我们它换成了关于x的表达式并将幂指数x换成了 “线性函数”表达式。H(x) 的函数图像呈现 S 形分布从而能够预测出离散的输出结果。 LogIstic 回归算法的损失函数有点复杂也许你会感动莫名其妙损失函数的表达式如下 L ( x ) − y l o g H ( x ) − ( 1 − y ) l o g ( 1 − H ( x ) ) L(x)-ylogH(x)-(1-y)log(1-H(x)) L(x)−ylogH(x)−(1−y)log(1−H(x))
5.KNN最邻近分类算法 为了判断未知样本的类别以所有已知类别的样本作为参照来计算未知样本与所有已知样本的距离然后从中选取与未知样本距离最近的 K 个已知样本并根据少数服从多数的投票法则majority-voting将未知样本与 K 个最邻近样本中所属类别占比较多的归为一类。这就是 KNN 算法基本原理。 KNN 算法原理如果一个样本在特征空间中存在 K 个与其相邻的的样本其中某一类别的样本数目较多则待预测样本就属于这一类并具有这个类别相关特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN 算法简单易于理解无须估计参数与训练模型适合于解决多分类问题。但它的不足是当样本不平衡时如一个类的样本容量很大而其他类样本容量很小时有很能导致当输入一个新样本时该样本的 K 个邻居中大容量类的样本占多数而此时只依照数量的多少去预测未知样本的类型就会可能增加预测错误概率。此时我们就可以采用对样本取“权值”的方法来改进。 下面对 KNN 算法的流程做简单介绍。KNN 分类算法主要包括以下 4 个步骤
准备数据对数据进行预处理 。计算测试样本点也就是待分类点到其他每个样本点的距离选定度量距离的方法对每个距离进行排序然后选择出距离最小的 K 个点。对K 个点所属的类别进行比较按照少数服从多数的原则多数表决思想将测试样本点归入到 K 个点中占比最高的一类中。
6.朴素贝叶斯分类算法 贝叶斯定理的发明者 托马斯·贝叶斯 提出了一个很有意思的假设“如果一个袋子中共有 10 个球分别是黑球和白球但是我们不知道它们之间的比例是怎么样的现在仅通过摸出的球的颜色是否能判断出袋子里面黑白球的比例” 上述问题可能与我们高中时期所接受的的概率有所冲突因为你所接触的概率问题可能是这样的“一个袋子里面有 10 个球其中 4 个黑球6 个白球如果你随机抓取一个球那么是黑球的概率是多少”毫无疑问答案是 0.4。这个问题非常简单因为我们事先知道了袋子里面黑球和白球的比例所以很容易算出摸一个球的概率但是在某些复杂情况下我们无法得知“比例”此时就引出了贝叶斯提出的问题。 在统计学中有两个较大的分支一个是“频率”另一个便是“贝叶斯”它们都有各自庞大的知识体系而“贝叶斯”主要利用了“相关性”一词。下面以通俗易懂的方式描述一下“贝叶斯定理”通常事件 A 在事件 B 发生的条件下与事件 B 在事件 A 发生的条件下它们两者的概率并不相同但是它们两者之间存在一定的相关性并具有以下公式称之为“贝叶斯公式”
7.决策树分类算法
8.信息熵
9.支持向量机SVM分类算法 emsp;emsp;支持向量机英文全称“Support Vector Machines”简称 SVM它是机器学习中最常用的一种“分类算法”。SVM 是一种非常优雅的算法有着非常完善的数学理论基础其预测效果在众多机器学习模型中可谓“出类拔萃”。在深度学习没有普及之前“支持向量机”可以称的上是传统机器学习中的“霸主”下面我们将介绍本节的主人公——支持向量机SVM。emsp;emsp; 支持向量机是有监督学习中最有影响力的机器学习算法之一该算法的诞生可追溯至上世纪 60 年代 前苏联学者 Vapnik 在解决模式识别问题时提出这种算法模型此后经过几十年的发展直至 1995 年 SVM 算法才真正的完善起来其典型应用是解决手写字符识别问题。